El número áureo o de oro (también llamado número dorado, razón áurea, razón dorada, media áurea, proporción áurea y divina proporción). Número esta representado por la letra griega Φ (fi), en honor al escultor griego Fidas.
el numero aureo es es siguiente numero irracional.
Este número posee muchas propiedades interesantes y fue descubierto como una relacion de segmentos en la antiguedad.
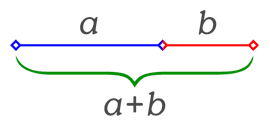
La sección áurea es una división en dos de un segmento según proporciones dadas por el número áureo. La longitud total a+b es al segmento más largo a como a es al segmento más corto b.
Pero aqui nos centraremos en numerar algunas de las curiosidades de este numero con la vida cotidiana, el arte e incluso el cuerpo humano. el numero aureo, esta continuamente presente en nuestra vida, desde nuestros documentos de identidad hasta relaciones dentro de nuestro propio cuerpo. algunos ejemplos de las relaciones anatomicas con este numero son:
- La relación entre nuestra altura y la altura de nuestro ombligo.
- La relación entre la distancia del hombro a los dedos y la distancia del codo a los dedos.
- La relación entre el primer hueso de los dedos (metacarpiano) y la primera falange, o entre la primera y la segunda, o entre la segunda y la tercera, si dividimos todo es Φ.
- La relación entre el diámetro de la boca y el de la nariz.
Aparte de estas sorprendentes relaciones en nuestro cuerpo la relación áurea también esta presente en el arte, como por ejemplo en el Partenón Griego.
En esta figura se puede comprobar que AB/CD= Φ. Hay más cocientes entre sus medidas que dan el número áureo, por ejemplo: AC/AD= Φ y CD/CA= Φ. Aunque si investigamos, podemos encontrar un precedente al uso de esta relación áurea en el arte griego, y esto lo podemos encontrar en el antiguo Egipcio. Este ejemplo es la Gran Pirámide de Keops, donde el cociente entre la altura de uno de los triángulos que forman esta pirámide con su lado es de 2 Φ.
Una de las relaciones mas famosas de una obra de arte con el numero áureo es el Hombre de Vitruvio, de Leonardo Da Vinci. Las relaciones entre las articulaciones del Hombre de Vitruvio son el número áureo. Estas relaciones, ademas, son observables en el resto de las obras de Da Vinci. Esta obra ademas nos introduce al termino del "hombre perfecto"cuyas relaciones entre las distintas partes del cuerpo serian el numero áureo.
Estirando manos y pies y haciendo centro en el ombligo se dibuja la circunferencia. El cuadrado tiene por lado la altura del cuerpo que coincide, en un cuerpo armonioso, con la longitud entre los extremos de los dedos de ambas manos cuando los brazos están extendidos y formando un ángulo de 90º con el tronco. Resulta que el cociente entre la altura del hombre (lado del cuadrado) y la distancia del ombligo a la punta de la mano (radio de la circunferencia) es el número áureo.
El rostro humano no se libra de estas relaciones, segun Da vinci la belleza estaba relacionada con su cercania a esta relación, por tanto la disposicion de los elementos de un rostro y sus distancias hacen que cuanto mas se paroximaran estas relaciones a Φ mas bello es el rostro.
Estas relaciones tienen mucha importancia en el ambito policial, ya que con la tecnologia actual, en el caso de tener imagenes de un delincuente, se le puede identificar por las relaciones entre los elementos de su rostro, ya que estas son unicas en cada persona. Por lo cual la cara ha pasado a ser una especia de "huella dactilar" con la que se puede identificar a una persona aunque cambie de aspecto.
En la naturaleza tambien encontramos esta relación áurea, uno de estos ejemplos es la espiral logaritmica, donde encontramos uno de los casos mas curiosos de relacion con el numero aureo.
Si tomamos un rectángulo áureo ABCD y le sustraemos el cuadrado AEFD cuyo lado es el lado menor AD del rectángulo, resulta que el rectángulo EBCF es áureo. Si después a éste le quitamos el cuadrado EBGH, el rectángulo resultante HGCF también es áureo. Este proceso se puede reproducir indefinidamente, obteniéndose una sucesión de rectángulos áureos encajados que convergen hacia el vértice O de una espiral logarítmica.
La espiral logarítmica vinculada a los rectángulos áureos gobierna el crecimiento armónico de muchas formas vegetales (flores y frutos) y animales (conchas de moluscos), aquellas en las que la forma se mantiene invariante. El ejemplo más visualmente representativo es la concha del nautilus.
Es curioso pero hasta las tarjetas de crédito o nuestro carnet de identidad tienen el número áureo incrustado en si mismos, el largo y ancho de esos elementos guardan una relación. Y esto no es porque si, sino porque al parecer nuestra capacidad perceptiva se acomoda mas fácilmente a estas dimensiones.